1. lappusē - Aksonometrisko projekciju asis.

2. lappusē - Punkta projekcijas 1. un 2. piemērs.

3. lappusē - Punkta projekcijas 3. piemērs.

 

Aksonometrisko projekciju asis

Lai izprastu, kā tehniskajā grafikā tiek pielietota taisnleņķa projicēšanas metode, jāsāk ar vieglāko, tāpēc vispirms jāapskata punkta projekcijas.

Jebkurš punkts atrodas telpā. Kā telpa rasējumā tiek izmantots trīsplakņu kakts, kuru veido X, Y un Z asis (1). Šīs asis sauc par aksonometriskajām asīm. Uz aksonometriskajām asīm tiek atliktas punkta koordinātas. Piemēram, ja dots A (40; 30; 60), tas nozīmē, ka punktam A ir šādas koordinātas: x=40mm; y=30mm; z=60mm (2). 

       

1                                                                                 2

Turpinājums ...

Priekšmeta attēlu plaknē (uz papīra vai tāfeles) iegūst, izmantojot projicēšanu. Izšķir centrālo un paralēlo projicēšanu.

Centrālā projicēšana (1) ir tad, ja visi projicējošie stari, kas veido priekšmeta (ABCD) attēlu (abcd), iziet no viena punkta. Šāda veida projekcijas bieži sauc par perspektīvu. Priekšmeta forma un izmērs centrālajā projekcijā attēlojas sagrozīti.

1

 

Turpinājums ...

1. lappusē - Ovāli.

2. lappusē - Ovoīdi.

3. lappusē - Spirāllīknes.

 

Cirkuļlīknes ir līknes, kuras veido riņķa līniju loki ar dažādiem rādiusiem. Pie cirkuļlīknēm pieder ovāli, ovoīdi un spirāllīknes.

 

Ovāls

 

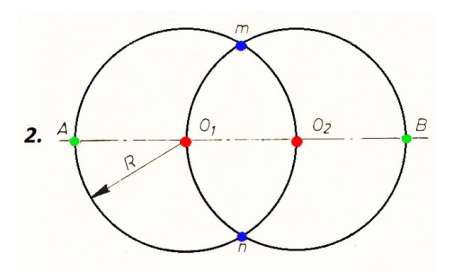
1. veids. Dota ovāla garākā ass AB.

1. Asi AB sadala 3 vienādās daļās (AO1; O1O2; O2B).

2. Ar rādiusu R, kas vienāds ar attālumu O1O2, caur centriem O1 un O2 velk riņķa līnijas, kuras krustojas punktos m un n.

Turpinājums ...

1. lappusē - Divu taišņu salaidums.

2. lappusē - Taisnes un riņķa līnijas salaidums.

3. lappusē - Divu riņķa līniju saskare un salaidums.

 

Mehānismos ir tādas detaļas, kuru kontūras veido taisnes un riņķu loki, kas laideni pāriet cits citā. Lai konstruētu šādas pārejas, rasējumos lieto salaidumus. Izšķir divu taišņu salaidumus; taisnes un riņķa līnijas salaidumus un divu riņķa līniju salaidumus.

 

Divu taišņu salaidums

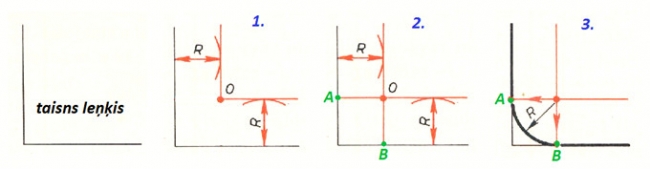
Dotas divas taisnes, leņķis starp tām un salaiduma loka rādiuss R.

1. Paralēli abām taisnēm attālumā R no tām novelk taisnes, kuru krustpunkts ir salaiduma centrs O.

2. No salaiduma centra O velk perpendikulus pret abām taisnēm, iegūstot salaiduma punktus A un B.

3. Novieto cirkuļa kājiņu salaiduma centrā O un starp salaiduma punktiem A un B novelk loku ar rādiusu R.

 

Turpinājums ...